Predict Concentration Using Calibration

Predict concentration using a calibration line (or curve) and inverse regression.

inversePredictCalibrate(object, obs.y = NULL, 
    n.points = ifelse(is.null(obs.y), 100, length(obs.y)), 
    intervals = FALSE, coverage = 0.99, simultaneous = FALSE, 
    individual = FALSE, trace = FALSE)

Arguments

object: an object of class "calibrate" that is the result of calling the function
calibrate.
obs.y: optional numeric vector of observed values for the machine signal. The default value is obs.y=NULL, in which case obs.y is set equal to a vector of values (of length n.points) ranging from the minimum to the maximum of the fitted values from the calibrate object.
n.points: optional integer indicating the number of points at which to predict concentrations (i.e., perform inverse regression). The default value is n.points=100. This argument is ignored when obs.y is supplied.
intervals: optional logical scalar indicating whether to compute confidence intervals for the predicted concentrations. The default value is intervals=FALSE.
coverage: optional numeric scalar between 0 and 1 indicating the confidence level associated with the confidence intervals for the predicted concentrations. The default value is coverage=0.99.
simultaneous: optional logical scalar indicating whether to base the confidence intervals for the predicted values on simultaneous or non-simultaneous prediction limits. The default value is simultaneous=FALSE.
individual: optional logical scalar indicating whether to base the confidence intervals for the predicted values on prediction limits for the mean (individual=FALSE) or prediction limits for an individual observation (individual=TRUE). The default value is individual=FALSE.
trace: optional logical scalar indicating whether to print out (trace) the progress of the inverse prediction for each of the specified values of obs.y. The default value is trace=FALSE.

Details

A simple and frequently used calibration model is a straight line where the response variable \(S\) denotes the signal of the machine and the predictor variable \(C\) denotes the true concentration in the physical sample. The error term is assumed to follow a normal distribution with mean 0. Note that the average value of the signal for a blank (\(C = 0\)) is the intercept. Other possible calibration models include higher order polynomial models such as a quadratic or cubic model.

In a typical setup, a small number of samples (e.g., \(n = 6\)) with known concentrations are measured and the signal is recorded. A sample with no chemical in it, called a blank, is also measured. (You have to be careful to define exactly what you mean by a “blank.” A blank could mean a container from the lab that has nothing in it but is prepared in a similar fashion to containers with actual samples in them. Or it could mean a field blank: the container was taken out to the field and subjected to the same process that all other containers were subjected to, except a physical sample of soil or water was not placed in the container.) Usually, replicate measures at the same known concentrations are taken. (The term “replicate” must be well defined to distinguish between for example the same physical samples that are measured more than once vs. two different physical samples of the same known concentration.)

The function calibrate initially fits a linear calibration line or curve. Once the calibration line is fit, samples with unknown concentrations are measured and their signals are recorded. In order to produce estimated concentrations, you have to use inverse regression to map the signals to the estimated concentrations. We can quantify the uncertainty in the estimated concentration by combining inverse regression with prediction limits for the signal \(S\).

Value

A numeric matrix containing the results of the inverse calibration. The first two columns are labeled obs.y and pred.x containing the values of the argument obs.y and the predicted values of x (the concentration), respectively. If intervals=TRUE, then the matrix also contains the columns lpl.x and upl.x corresponding to the lower and upper prediction limits for x. Also, if intervals=TRUE, then the matrix has the attributes coverage (the value of the argument coverage) and simultaneous (the value of the argument simultaneous).

References

Currie, L.A. (1997). Detection: International Update, and Some Emerging Di-Lemmas Involving Calibration, the Blank, and Multiple Detection Decisions. Chemometrics and Intelligent Laboratory Systems 37, 151–181.

Draper, N., and H. Smith. (1998). Applied Regression Analysis. Third Edition. John Wiley and Sons, New York, Chapter 3 and p.335.

Hubaux, A., and G. Vos. (1970). Decision and Detection Limits for Linear Calibration Curves. Annals of Chemistry 42, 849–855.

Millard, S.P., and N.K. Neerchal. (2001). Environmental Statistics with S-PLUS. CRC Press, Boca Raton, FL, pp.562–575.

Author

Steven P. Millard (EnvStats@ProbStatInfo.com)

Note

Almost always the process of determining the concentration of a chemical in a soil, water, or air sample involves using some kind of machine that produces a signal, and this signal is related to the concentration of the chemical in the physical sample. The process of relating the machine signal to the concentration of the chemical is called calibration (see calibrate). Once calibration has been performed, estimated concentrations in physical samples with unknown concentrations are computed using inverse regression. The uncertainty in the process used to estimate the concentration may be quantified with decision, detection, and quantitation limits.

In practice, only the point estimate of concentration is reported (along with a possible qualifier), without confidence bounds for the true concentration \(C\). This is most unfortunate because it gives the impression that there is no error associated with the reported concentration. Indeed, both the International Organization for Standardization (ISO) and the International Union of Pure and Applied Chemistry (IUPAC) recommend always reporting both the estimated concentration and the uncertainty associated with this estimate (Currie, 1997).

Examples

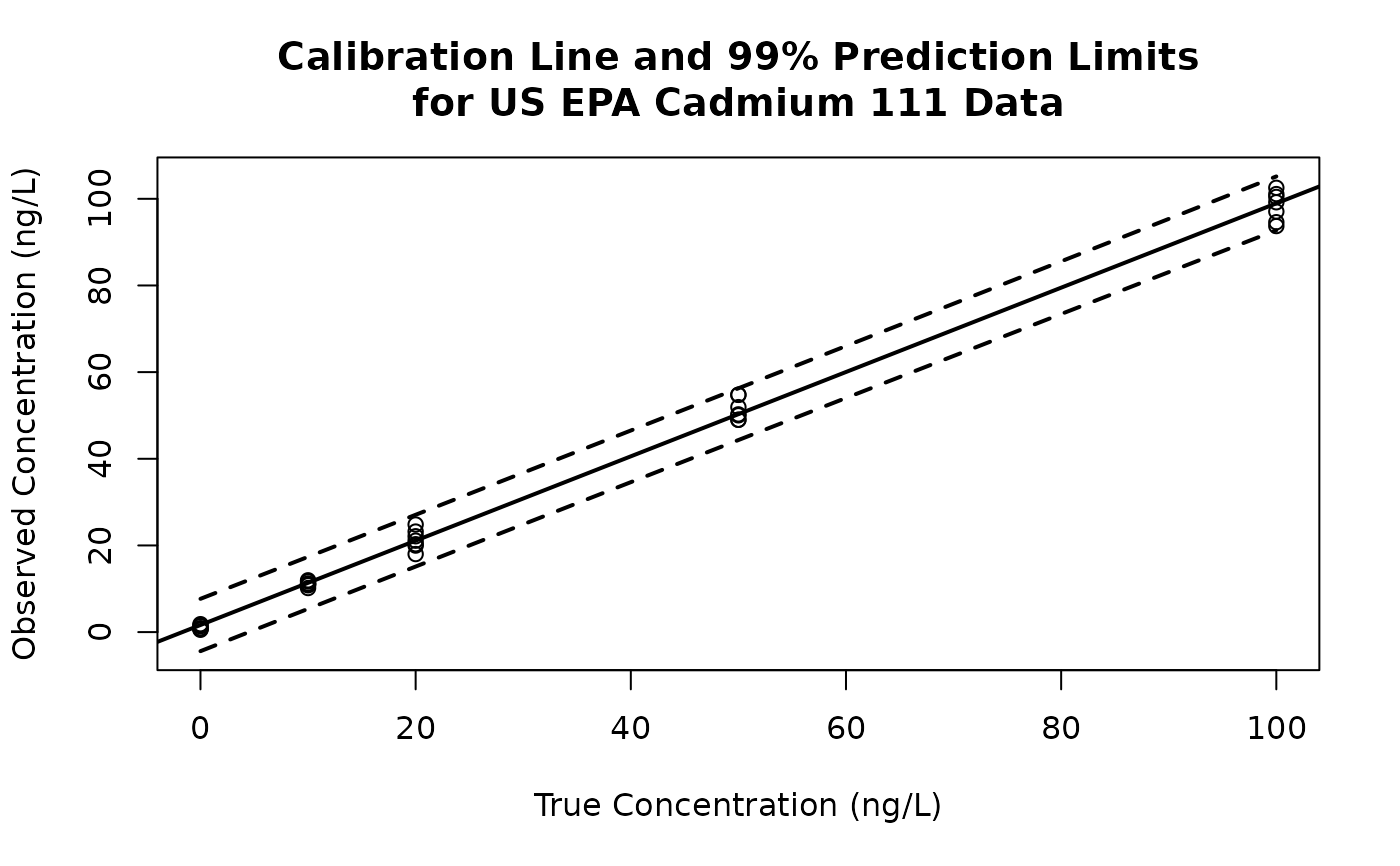
  # The data frame EPA.97.cadmium.111.df contains calibration data 
  # for cadmium at mass 111 (ng/L) that appeared in 
  # Gibbons et al. (1997b) and were provided to them by the U.S. EPA.  
  # Here we 
  # 1. Display a plot of these data along with the fitted calibration 
  #    line and 99% non-simultaneous prediction limits. 
  # 2. Then based on an observed signal of 60 from a sample with 
  #    unknown concentration, we use the calibration line to estimate 
  #    the true concentration and use the prediction limits to compute 
  #    confidence bounds for the true concentration. 
  # An observed signal of 60 results in an estimated value of cadmium 
  # of 59.97 ng/L and a confidence interval of [53.83, 66.15]. 
  # See Millard and Neerchal (2001, pp.566-569) for more details on 
  # this example.

  Cadmium <- EPA.97.cadmium.111.df$Cadmium 

  Spike <- EPA.97.cadmium.111.df$Spike 

  calibrate.list <- calibrate(Cadmium ~ Spike, 
    data = EPA.97.cadmium.111.df) 

  newdata <- data.frame(Spike = seq(min(Spike), max(Spike), 
    length.out = 100))

  pred.list <- predict(calibrate.list, newdata = newdata, se.fit = TRUE) 

  pointwise.list <- pointwise(pred.list, coverage = 0.99, 
    individual = TRUE)

  plot(Spike, Cadmium, ylim = c(min(pointwise.list$lower), 
    max(pointwise.list$upper)), xlab = "True Concentration (ng/L)", 
    ylab = "Observed Concentration (ng/L)") 

  abline(calibrate.list, lwd=2) 

  lines(newdata$Spike, pointwise.list$lower, lty=8, lwd=2) 

  lines(newdata$Spike, pointwise.list$upper, lty=8, lwd=2) 

  title(paste("Calibration Line and 99% Prediction Limits", 
    "for US EPA Cadmium 111 Data", sep = "\n")) 


 
  # Now estimate the true concentration based on 
  # an observed signal of 60 ng/L. 

  inversePredictCalibrate(calibrate.list, obs.y = 60, 
    intervals = TRUE, coverage = 0.99, individual = TRUE) 
#>      obs.y   pred.x   lpl.x    upl.x
#> [1,]    60 59.97301 53.8301 66.15422
#> attr(,"coverage")
#> [1] 0.99
#> attr(,"simultaneous")
#> [1] FALSE

  #     obs.y   pred.x   lpl.x    upl.x 
  #[1,]    60 59.97301 53.8301 66.15422 
  #attr(, "coverage"): 
  #[1] 0.99 
  #attr(, "simultaneous"): 
  #[1] FALSE

  rm(Cadmium, Spike, calibrate.list, newdata, pred.list, pointwise.list)